Session 1.1

Causal questions and counterfactuals in pregnancy research Intro to R

Louisa Smith

Hello!

Workshop goals

• Understand how theory gets implemented in code
  • I’ve tried to integrate them
• Take away code snippets, but with ability to understand how to modify
• Know where to look in the literature
• Open time to practice/ask questions

‎

Everyone is coming with a different background, so some things will likely be a review. Hopefully even if you’ve seen these topics before you will be thinking about them in a new or deeper way!

Daily schedule

Time	Activity
09:30–10:30	Session Block 1
10:30–11:00	Tea/Coffee break
11:00–12:00	Session Block 2
12:00–13:00	Lunch
13:00–14:00	Session Block 3
14:00–14:30	Tea/Coffee break
14:30–15:30	Q&A/Office Hours

Resources (R)

R can be overwhelming if you’re not used to it

I teach a couple of short courses on R (for you to peruse later)

• intro course: https://id543.louisahsmith.com/
• intermediate course: https://epi590r.louisahsmith.com/

These also link to more resources that may be helpful

Why this topic?

What makes pregnancy research challenging? (an incomplete list!)

1. Time-varying exposures during gestational development with varying relationships to outcomes
2. Competing events (e.g., conception, pregnancy loss)
3. Outcomes that often depend on duration of pregnancy or exposure during pregnancy
4. Exposure timing during pregnancy can create immortal time bias
5. Multiple individuals (pregnancy, fetus, child)

Some (but maybe not all) of these problems can be addressed with…

• Careful specification of a causal question
• Analysis that matches the question

‎

Miguel Hernán’s two-step algorithm for causal inference: Ask a causal question. Answer the causal question.

What are causal questions?

A second chance to get causal inference right: a classification of data science tasks Hernán, Hsu, and Healy (2019)

What proportion of pregnant people received COVID-19 vaccination during pregnancy in 2023?

How many preterm births occurred among women with gestational diabetes in our hospital last year?

What is the probability of preterm birth for a 35-year-old nulliparous woman with gestational diabetes?

How can we best guess which pregnancies will result in low birth weight based on first trimester characteristics?

Does COVID-19 vaccination during pregnancy reduce the risk of severe maternal illness compared to no vaccination?

Would discontinuing antidepressants during pregnancy reduce birth defect risk compared to continuing them?

description

What proportion of pregnant people received COVID-19 vaccination during pregnancy in 2023?

How many preterm births occurred among women with gestational diabetes in our hospital last year?

prediction

What is the probability of preterm birth for a 35-year-old nulliparous woman with gestational diabetes?

How can we best guess which pregnancies will result in low birth weight based on first trimester characteristics?

causation

Does COVID-19 vaccination during pregnancy reduce the risk of severe maternal illness compared to no vaccination?

Would discontinuing antidepressants during pregnancy reduce birth defect risk compared to continuing them?

Questions of causation generally involve changing something

• Does COVID-19 vaccination during pregnancy reduce the risk of severe maternal illness vs. no vaccination during pregnancy?
• Would discontinuing antidepressants during pregnancy reduce birth defect risk vs. continuing them?
  • These questions involve comparing different interventions
  • Note: I will refer to what is changed as “intervention” or “exposure” or “treatment” or “treatment strategy” basically interchangeably
• Contrast with: “What is the association between maternal age and preterm birth?”
  • We’re not asking what would happen if we could change maternal age, but describing what the world actually looks like
  • (We could ask a causal question about age, for example if we asked people to delay pregnancy until a different age…)

Counterfactual notation makes this clear

What would have happened under different treatment scenarios?

If \(Y\) is our factual (observed) outcome of interest:

• \(Y^1\): Outcome if someone receives treatment
• \(Y^0\): Outcome if someone does not receive treatment

More generally: \(Y^a\) = outcome under treatment scenario \(A = a\)

Pregnancy examples of counterfactuals

• \(Y^{\text{vaccinated}}\): Preterm birth if vaccinated during pregnancy
• \(Y^{\text{unvaccinated}}\): Preterm birth if not vaccinated during pregnancy

The fundamental problem of causal inference

We can only observe one potential outcome per person:

ID	Vaccinated	Y	\(Y^{\text{vacc}}\)	\(Y^{\text{unvacc}}\)
1	0	Preterm	???	Preterm
2	1	Preterm	Preterm	???
3	1	Term	Term	???
4	0	Term	???	Term

Missing data problem: Causal inference is about estimating the missing potential outcomes using data from people with observed outcomes

The fundamental problem of causal inference

We can only observe one potential outcome per person:

ID	Vaccinated	Observed	\(Y^{\text{vacc}}\)	\(Y^{\text{unvacc}}\)
1	0	Preterm	???	Preterm
2	1	Preterm	Preterm	???
3	1	Term	Term	???
4	0	Term	???	Term

• Consider something like matching, where we would match a vaccinated with an unvaccinated person with similar characteristics (confounders) to estimate the missing potential outcomes for each

But what does the variable “Vaccinated” mean? How can we be sure that we make a fair comparison?

A common pregnancy question

“If I use this treatment during pregnancy, do I have an increased risk of some outcome?”

Problems with this question:

• Implied comparison is with “expected risk in population”
• Doesn’t specify when treatment is used
• Doesn’t define the alternative strategy
• Could be descriptive rather than causal

Huybrechts, Bateman, and Hernández-Díaz (2025)

A better pregnancy causal question

“If I use this treatment during pregnancy, do I have an increased risk relative to if I had not used it?”

This translates to: “What is the average risk in people like me who use the medication relative to the risk in an identical group who do not?”

Huybrechts, Bateman, and Hernández-Díaz (2025)

But we need to be even more specific

Among users:

• What is the risk for discontinuation of the drug vs. continuation?
• What is the risk for switching to a different drug vs. continuation?

Among non-users (or former users):

• What is the risk for initiation of the drug vs. no treatment?

All compared to an identical population who does something different.

Huybrechts, Bateman, and Hernández-Díaz (2025)

And we need to be specific about timing

• When trying to become pregnant?
• At a specific gestational age?
• When certain clinical characteristics are met?

The comparison population might do the same thing but at a different time (e.g., effect of earlier vs. later treatment), might do a different thing (e.g., treatment with a different drug), might do the same thing but more/less (different dose or duration), or might not do anything at all (but could have!)

More precise counterfactuals

We can be more specific:

• \(T^{x=12}\): Gestational age at delivery if vaccinated at 12 weeks
• \(T^{x=22}\): Gestational age at delivery if vaccinated at 22 weeks
• \(T^{x\neq12}\): Gestational age at delivery if not vaccinated at 12 weeks (do anything you want, as long as not that?!)

‎

Notice that we’re being more specific with the outcome as well, to allow us to study effects across gestational duration

This makes what we know and don’t know a little more complicated

ID	Vaccination week	T	\(T^{x=12}\)	\(T^{x=22}\)	\(T^{x\neq12}\)
5	Never	11	11	11	11
6	Never	14	???	14	14
7	12	18	18	???	???
8	34	40	???	???	???

We will see how to figure out what counterfactuals we can estimate

• Target trial emulation helps us specify exactly which counterfactuals we want to estimate
• Different research questions require different counterfactuals
  
• Not all counterfactuals are identifiable from observational data
• The choice affects both study design and analysis approach

Exercises are in Quarto documents

• Quarto is a publishing system that combines text, code, and output
  • Built into RStudio (new-ish versions)
  • Similar to R Markdown but with enhanced features
  • Files end in .qmd
• Code goes in “chunks” surrounded by three backticks (chunks will be a slightly different color in RStudio)
  • Text is written in Markdown in between chunks
  • You can run individual chunks or render the whole document
• Output appears below each chunk when you render it

‎

These slides are made in quarto too, so I can generate output using R code!

First code chunk: set-up

I asked you to install some packages with install.packages()

• It’s not a problem if you didn’t, but you will have to install them before running the code
• Running install.packages("packagename") will install the most recent version of the package to ensure you get the same results as me

If you don’t have a package installed, you may see this (you can click Install!)

First code chunk: set-up

Every time you start a new R session (which I suggest you do often, including with every new set of exercises), you need to load the packages with library(packagename)

library(tidyverse)
library(gtsummary)

I also set a ggplot theme at the top, so it applies to all figures

theme_set(theme_minimal())

What you’ll actually see

• Visual mode
• Source mode

You can run the whole chunk at once with the green “play” button, or run line-by-line with Cmd+Enter (Mac) or Ctrl+Enter (Windows)

We are going to read in some simulated data

I made more than we need, so we are just going to sample n = 10,000 pregnancies, but we may change that as we go

# set random seed for reproducibility
set.seed(12345)
# read in data
dat <- read_rds("simulated_data.rds") |> 
    # select random 10,000 pregnancies
    sample_n(10000)

Setting the seed ensures that we get the same random sample each time we run this code

Where did the data come from?

• Baseline covariates were generated to reflect real-world Norwegian registry data
• I used the literature to inform the distribution of pregnancy duration starting at 6 weeks’ gestation and randomly assigned a length to each pregnancy
• Some time-varying covariates and birthweight were generated based on a model using the baseline covariates and gestational duration
• Spontaneous abortions and preterm births were defined based on gestational duration
• Stillbirth was assigned randomly among pregnancies that reached 20 weeks’ gestation

‎

The data is somewhat but not totally realistic

Data dictionary (baseline)

Variable Name	Description
ID	Unique pregnancy identifier
maternal_age	Maternal age at conception (years)
BMI_b4preg	Pre-pregnancy body mass index (kg/m²)
Riskfactors	Pre-existing risk factors (low vs. moderate or high)
educ	Educational level (low vs. high)
nullparity	Nulliparity (1 if first pregnancy, 0 if multiparous)
country_birth	Country of birth (Scandinavia vs. Outside Scandinavia)

Data dictionary (pregnancy)

Variable Name	Description
bleeding_beforeWk13	Bleeding before week 13 (0/1)
bleeding_week13_28	Bleeding between weeks 13 and 28 (0/1)
bleeding_afterWk28	Bleeding after week 28 (0/1)
gest_week	Gestational age at delivery/pregnancy end (weeks)
gest_days	Gestational age at delivery/pregnancy end (days)
sab	Spontaneous abortion (1 if pregnancy ended <20 weeks, 0 otherwise)
stillbirth	Stillbirth (1 if fetal death ≥20 weeks, 0 if live birth, NA if SAB)
preterm	Preterm birth (1 if <37 weeks, 0 if ≥37 weeks, NA if SAB)
birthweight	Birth weight in grams (NA if SAB)
end_preg_event	Did we observe the pregnancy ending? (1 if yes, 0 if censored)

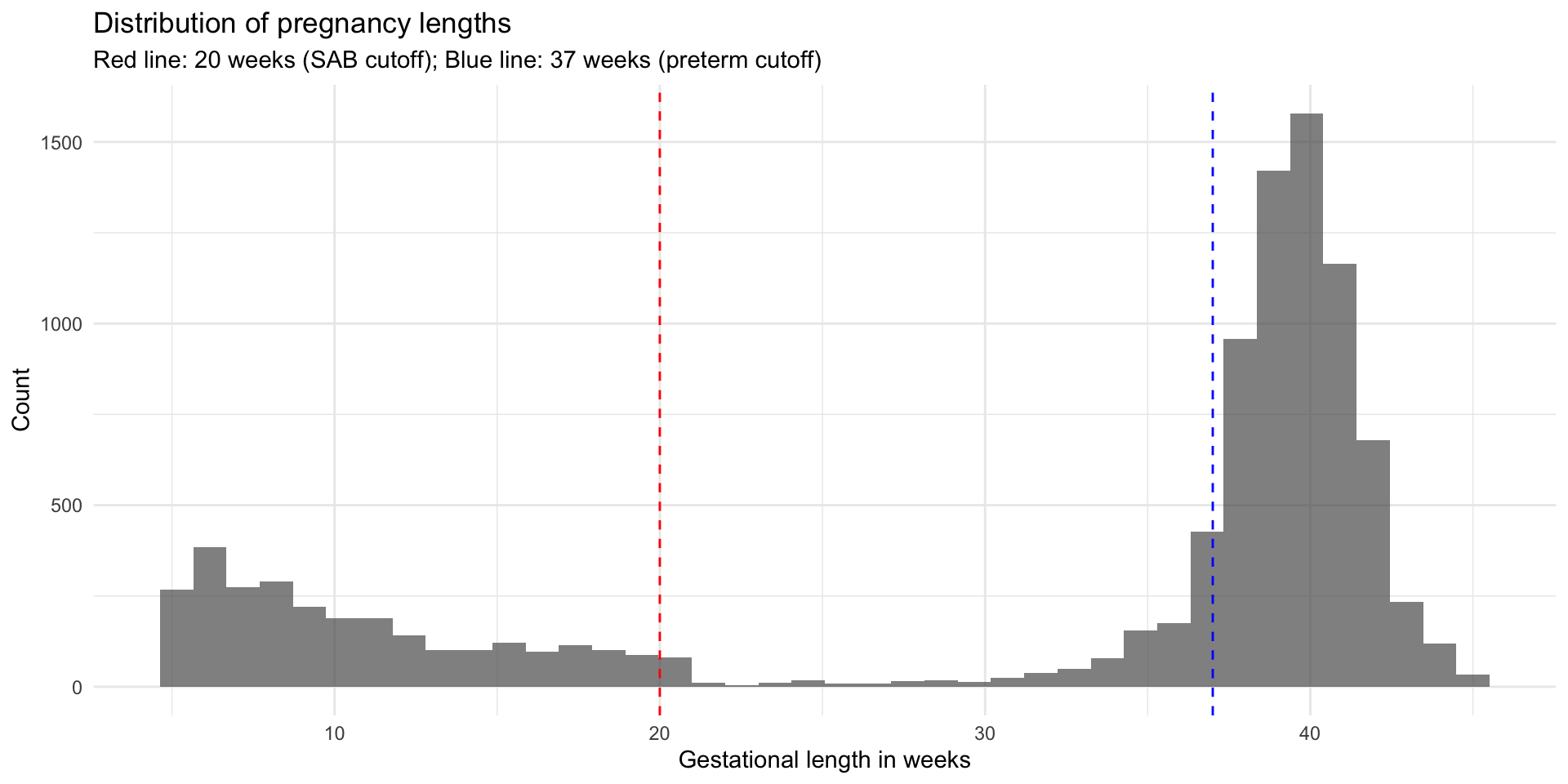
Let’s look at the data

# tell ggplot what data/variables to use
ggplot(dat, aes(gest_week)) +
  # add empirical cumulative distribution function
  stat_ecdf() +
  # add labels
  labs(
    y = "Cumulative probability of pregnancy ending",
    title = "Cumulative distribution function of pregnancy length"
  )

Let’s look at the data

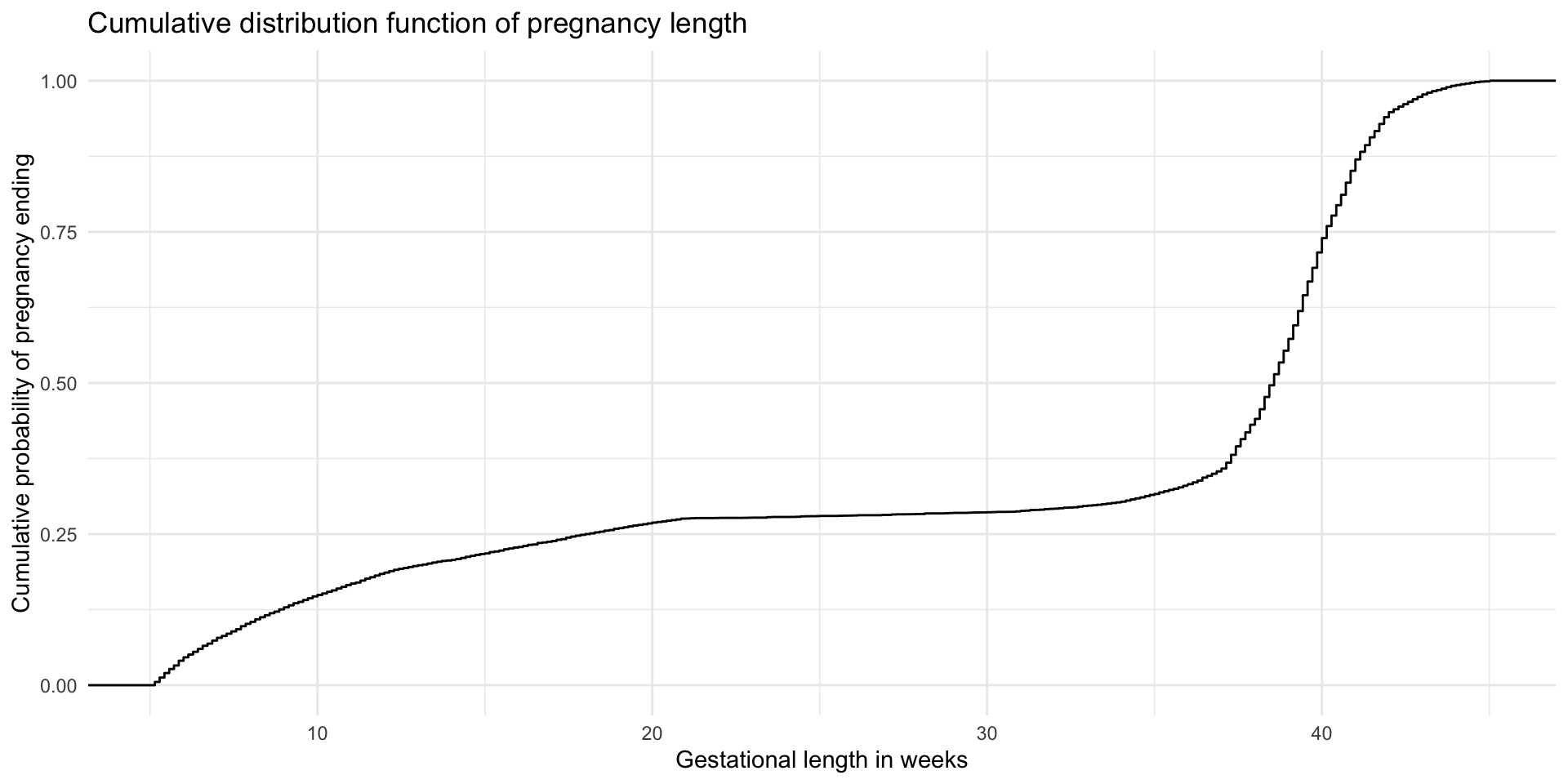
Let’s look at the data

# Look at pregnancy outcomes
tbl_cross(dat, sab, stillbirth)

	Stillbirth (>=20 weeks gestation)			Total
	0	1	Unknown
Spontaneous abortion (<20 weeks gestation)
0	7,194	130	0	7,324
1	0	0	2,676	2,676
Total	7,194	130	2,676	10,000

Let’s look at the data

# Look at pregnancy outcomes
ggplot(dat, aes(gest_week)) +
  geom_histogram(bins = 40, alpha = 0.7) +
  geom_vline(xintercept = 20, linetype = "dashed", color = "red") +
  geom_vline(xintercept = 37, linetype = "dashed", color = "blue") +
  labs(
    y = "Count",
    title = "Distribution of pregnancy lengths",
    subtitle = "Red line: 20 weeks (SAB cutoff); Blue line: 37 weeks (preterm cutoff)"
  )

Let’s look at the data

Exercises

Hernán, Miguel A., John Hsu, and Brian Healy. 2019. “A Second Chance to Get Causal Inference Right: A Classification of Data Science Tasks.” CHANCE 32 (1): 42–49. https://doi.org/10.1080/09332480.2019.1579578.

Huybrechts, Krista F., Brian T. Bateman, and Sonia Hernández-Díaz. 2025. “Modern Evidence Generation on Medication Effectiveness and Safety During Pregnancy: Study Design Considerations.” Clinical Pharmacology & Therapeutics 117 (4): 895–909. https://doi.org/10.1002/cpt.3598.